Conditional Simulation

Conditional simulation is a Monte Carlo-based method of producing multiple equally probable realisations of the potential grade values in a deposit.  The outcomes can be used to quantify resource/reserve uncertainty, assess economic risks, and assist decision-making under uncertainty.  The conditional simulation realisations shown below for a Ni laterite deposit have been generated from drill hole intercepts using a typical approach of assuming an average horizontal continuity.  In fact there is a strong undulating lateral continuity related to historical weathering depths.

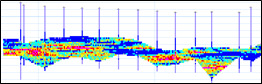
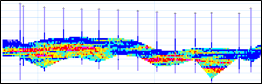
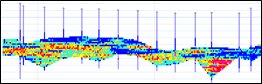
Unfolding

In instances where stratigraphic units have been subjected to folding, or where the mineralisation continuity does not follow a planar orientation along strike or down dip, standard methods of variography and interpolation using linear vectors in space often do not provide a good representation of continuity. One way to account for this would be to subdivide the deposit into domains of almost constant dip orientation and perform variography for each domain independently. However, this would probably result in very few sample pairs for some domains and be extremely time consuming. An alternative method, which ensures maximum correlation, uses an unfolding plane to relate samples from adjacent drill holes.

Advanced mining software packages provide unfolding for block grade estimation but not for conditional simulation due to the mathematical complexity of simulating grade values at large numbers of locations.

Conditional Simulation with Unfolding

Martlet Consultants have developed a simple method of conditional simulation with unfolding that involves no additional effort over the traditional approach other than to define a 2D or 3D unfolding surface. Examples of this new conditional simulation method for the Ni laterite deposit are shown below.

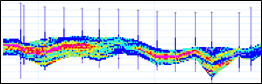
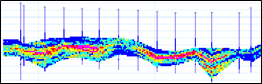
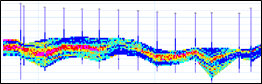
If you would like to discuss using conditional simulation with unfolding on your exploration or mining project please contact: Andrew Richmond

View pdf on Locating drill holes to reduce multivariate risk